which is equation of motions of the following standard form

For the formulation of standard form of the eigen value problem, equation (10.8)need to be transformed to the state space form as discussed in Chapter 5. The following example will illustrate the procedure of obtaining whirl natural frequencies for a typical case.

For the asynchronous whirl the eigen value problem of the form as equation(10.8) is not a standard one. For obtaining the standard form of the eigen value, equation(10.8) has to expressed in the state space form. To illustrate the transformation, let us consider the following simple example.

Example 10.1: Obtain the state space form of the following standard governing equation for vibrations of a spring-mass-damper system. Then obtain the frequency equation.

Solution : Let us express the velocity as

From equation (a), we get

Equations (b) and (c) which can be combined as

which can be written in the standard state space form, as

with

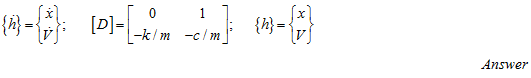
The solution of the above equation could be taken as

On substituting equation (f) into equation (e), we get

The frequency equation could be obtained as

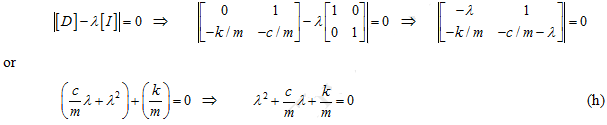
which is a familiar frequency equation for single-DOF spring-mass-damper system.

Answer.

Now coming back to conversion of equation(10.8) to the state space form, let

So that equation (10.8)takes the following form

Combining above two equations, we have