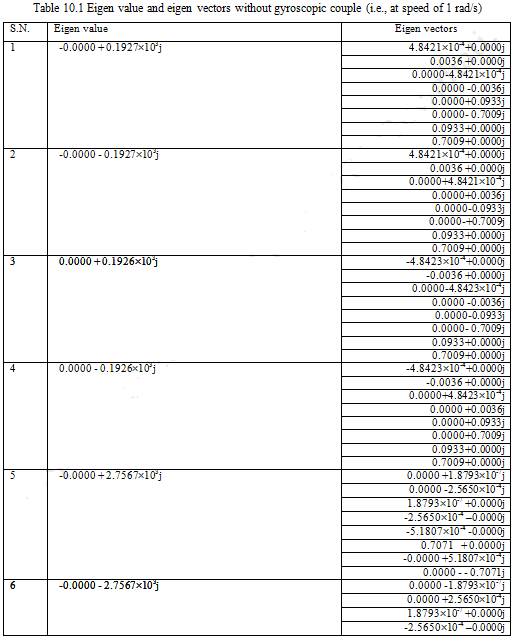
To compare eigen values and eigen vectors without and with gyroscopic effects the results from both the analysis are provided. Table 10.1 lists eigen values and eigen vectors corresponding to one element eigen analysis with 1 rad/s ( ~ 10 rpm, i.e. very slow speed) of rotor speed (i.e., negligible small gyroscopic effects). In eigen values the real part is related with the damping and the imaginary part is related with the natural whirl frequency of the system. It can be observed that the imaginary part of eigen value in serial numbers 1 to 4 are all the same. 1 and 2 are complex conjugate. Thus, the whirl frequency from serial number1 is positive and the whirl natural frequency from serial number 2 is exactly same with a negative sign. The negative frequency has no physical significance, hence, can be omitted. Without gyroscopic effect eigen value from serial numbers 1 and 3 are same, and eigen values from serial number 4 is complex conjugate of 3. Hence, actually there is only one natural whirl frequency (i.e., 192.68 rad/s see Table 10.1) from the first four eigen values. Similarly, from serial numbers 5 to 8 there is another natural whirl frequency (i.e., 1257.55 rad/s see Table 10.1). Hence, without gyroscopic effect case with one element we could be able to get only two natural frequencies (refer Table 10.3). Eigen vectors are also appearing in complex conjugate (see Table 10.1). It should be noted that with zero speed the dynamic matrix [D] becomes singular, since all the diagonal elements are zero with ![]() . Hence, it will be worthwhile to write the eigen value problem as
. Hence, it will be worthwhile to write the eigen value problem as
![]()
which is a familiar form as discussed in detail in Chapters 7 and 9 for respectively torsional and transverse vibrations.
The eigen value and eigen vector for matrix [D], for example, at 1500 rad/s, are provided in Table 10.2. It can be observed that these eigen values are also purely imaginary and occurring in complex conjugate (e.g., serial numbers: 1 and 2, 3 and 4, 5 and 6, and 7 and 8). Serial numbers 1 to 4 belong to the first natural mode (as in the case of without gyroscopic effects these are all same, however, now 1 and 3 are not same). Eigen values 2 and 4 are complex conjugate of eigen values 1 and 3, respectively; hence only eigen values 1 and 3 need to be considered (for the same reason as given for the case of without gyroscopic effects). Serial numbers 1 and 3 belong to the backward and forward whirls, respectively (which are below and above the first natural frequency without gyroscopic couple, i.e. 192.68 rad/s). Similarly serial numbers 5 and 7 belong to the backward and forward whirls, respectively (which are below and above the second natural frequency without gyroscopic couple , i.e. 1257.55 rad/s); and serial numbers 6 and 8 are exactly same as 5 and 7 with a negative sign (since real part in all eigen values are anyway zero).
Eigen vectors corresponding to these eigen values are also listed in Table 10.2. It can be observed that they are appearing as complex number. However, on close observation, it can be seen that either real part is zero or imaginary part is zero (e.g., for the eigen value 1, the real part of 1st and 2nd eigen vector components are zero, whereas, for the imaginary part of 3rd and 4th eigen vector components are zero. When the real part is zero the phase is 900 and when the real part is zero the phase is 00.