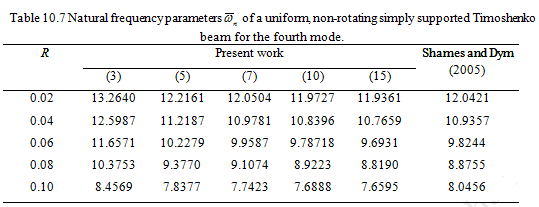
Due to the shear effect, deflection of the beam increases which reduces the effective stiffness. So the non-dimensionalised natural frequency decreases as the diameter of the beam is increased (i.e. with the slenderness ratio). This trend could be observed in all four modes. The accuracy of the present solution is well within 5% for all cases. By FEM we over-predict with coarser discretisation and it could be seen that as the number of elements are increased from 3 to 7 for first two modes and from 3 to 15 for the third and fourth modes the natural frequency parameter is decreasing. Especially converge (not much improvement) could be observed in Tabled 10.6 and 10.7 between the number of elements 10 to 15. The difference in the closed form solution of Shames and Dym (2005) and the FEM results could be due to the approximate nature of the eigen function ( chosen in the closed-form solution).

Example 10.3 A typical simply supported rotor disc system as shown in Figure 10.11 is to be analyzed for obtaining the whirl natural frequencies to show the application of the finite element method. Physical properties of the rotor system are given as: the diameter of shaft is 0.1m, the length of shaft is 3.5 m, the Young's modulus of material of shaft is 2.08×10 11 N/m², the mass density of the shaft material is 7830 kg/m³, the Poisson's ratio is 0.3, the number of rigid discs are 4, and the mass of each rigid disc is 60.3 kg.

Solution : The rotor is discretised into the seven and fourteen elements, respectively, as shown in Figures 10.11 and 10.12. In the case of seven elements, two identical rigid bearings are located at node numbers two and seven; and four rigid discs are located at node numbers three, four, five and six. In case of fourteen element member, two identical rigid bearings are located at node numbers three and thirteen, and rigid discs are located at node numbers five, seven, nine and eleven. The shaft is assumed uniform along the span.

Rigid discs are considered as point masses and these point masses are added to mass matrix corresponding to locations of rigid discs translational accelerations. The assembled mass and stiffness matrices are obtained by usual method and boundary conditions are applied to get the reduced form dynamic matrix. Natural whirl frequencies are obtained by solving eigen value problem. Natural whirl frequencies are obtained for 7 elements and 14 elements model and are given in Table 10.8. Results show that good convergence has already occurred with 7 elements model.