- Verify that the diagram (37.5) commutes.
- Determine
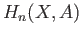 when
when
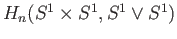 , and when
, and when  is a singleton and
is a singleton and 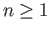 . What happens if
. What happens if 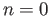 ?
?
- Compute
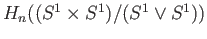 and compare it with the absolute homology
and compare it with the absolute homology
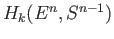 .
.
- Compute
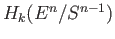 and compare it with
and compare it with
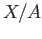 .
.
- In example (35.1), prove that
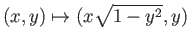 is homeomorphic to
is homeomorphic to
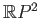 . Compare the groups
. Compare the groups 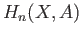 with the groups
with the groups 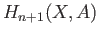 .
Hint: To set up the homeomorphism note that
.
Hint: To set up the homeomorphism note that
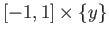 maps each
maps each
![$ [-1, 1]\times \{y\}$](img2980.png) homeomorphically onto the chord
at height
homeomorphically onto the chord
at height 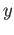 .
.
in
Lecture - XXXVIII Excision theorem
in
In this lecture we prove the most important theorem homology theory known as the excision theorem.
We shall conclude the lecture with the definition of local
homology groups that play an important role in the theory of orientability of topological manifolds.
We begin with the ubiquitous five lemma.
Subsections
nisha
2012-03-20
![$ [-1, 1]\times \{y\}$](img2980.png) homeomorphically onto the chord
at height
homeomorphically onto the chord
at height