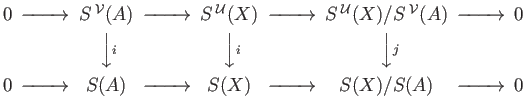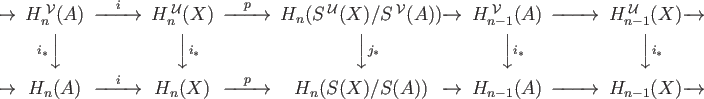The hypothesis implies that the pair
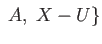 int
int is an open
cover of
is an open
cover of  , where
, where
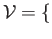 denotes the closure of
denotes the closure of  . Likewise
. Likewise
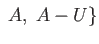 int
int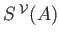 is an open cover of
is an open cover of  and
and
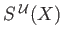 is a subcomplex of
is a subcomplex of
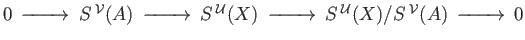 . By theorem (29.6) the short exact sequence of complexes
. By theorem (29.6) the short exact sequence of complexes
gives rise to a long exact sequence in homology:
On the other hand there is an obvious map of complexes induced by the inclusion maps namely
resulting in a commutative diagram of chain complexes
Since the long exact sequence in homology is natural (exercise 6 of lecture 29), we get the commutative diagram:
where we the subscript star indicates the map induced in homology. The five lemma enables us to conclude that
is an isomorphism. Note the inclusion
maps 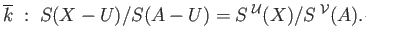 into
into
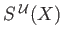 whereby we get an isomorphism (exercise 2)
whereby we get an isomorphism (exercise 2)
The composite
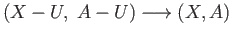 is also induced by the inclusion map
is also induced by the inclusion map
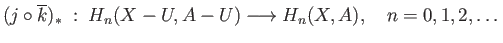 and
we have the desired isomorphism
and
we have the desired isomorphism
nisha
2012-03-20