Let 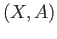 be a pair and
be a pair and  be a subset of
be a subset of  such that the closure of
such that the closure of  is
contained in the interior of
is
contained in the interior of  . Then, the homomorphism
. Then, the homomorphism
induced by inclusion
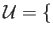 is an isomorphism for every
is an isomorphism for every
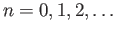 . In other words the set
. In other words the set  may be excised from the pair
may be excised from the pair 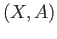 without affecting the homology groups of the pair.
without affecting the homology groups of the pair.
nisha
2012-03-20