We shall prove that 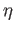 is injective, leaving surjectivity as an exercise.
Assume
is injective, leaving surjectivity as an exercise.
Assume
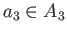 for some
for some
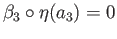 so that
so that
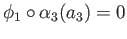 . The commutativity of the third
square now gives
. The commutativity of the third
square now gives
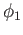 . Using injectivity of
. Using injectivity of 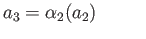 and exactness of the top row we arrive at
and exactness of the top row we arrive at
for some
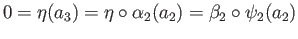 . Again,
. Again,
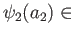 showing that
showing that
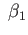 im
im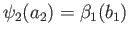 . Thus
. Thus
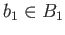 for some
for some
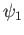 and using the surjectivity of
and using the surjectivity of
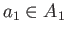 we get for some
we get for some
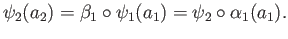 ,
,
Injectivity of 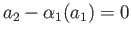 now gives
now gives
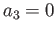 . Substituting into (38.1) we conclude
. Substituting into (38.1) we conclude 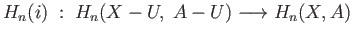 .
.
nisha
2012-03-20