Let 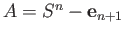 and
and
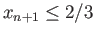 . We take
. We take  to be the complement of the
polar ice cap namely the set of all
to be the complement of the
polar ice cap namely the set of all
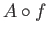 such that
such that
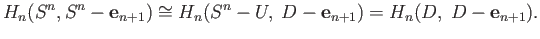 (reader is invited to draw a picture). Applying the excision theorem, and denoting the polar ice cap by
(reader is invited to draw a picture). Applying the excision theorem, and denoting the polar ice cap by 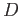 ,
,
Theorem (37.2) gives
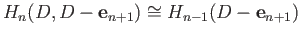 and
and
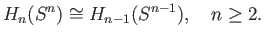 .
Since the polar ice cap is homeomorphic to an open ball,
.
Since the polar ice cap is homeomorphic to an open ball,
Using theorem (32.1) we conclude that
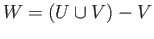 for
for 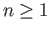 .
.
nisha
2012-03-20