Let us calculate the relative homology groups 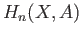 where
where  is the Möbius
band and
is the Möbius
band and  is its boundary. Since the central circle is a deformation retract of
is its boundary. Since the central circle is a deformation retract of  , we see that
, we see that
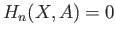 when
when 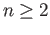 and we infer from (37.3) that
and we infer from (37.3) that
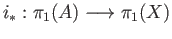 when
when 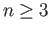 .
We now recall that the map
.
We now recall that the map
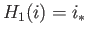 induced by inclusion is the group homomorphism of
induced by inclusion is the group homomorphism of
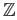 into itself given by
into itself given by
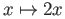 . Since the fundamental groups are abelian the map
. Since the fundamental groups are abelian the map
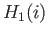 and so
the kernel of
and so
the kernel of 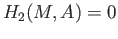 is trivial. The portion of the exact sequence (37.3) with
is trivial. The portion of the exact sequence (37.3) with 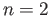 gives
gives
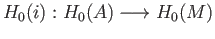 . Finally since
. Finally since
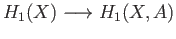 is an isomorphism (why?),
we conclude from
(37.3) (with
is an isomorphism (why?),
we conclude from
(37.3) (with 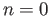 ) that the map
) that the map
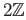 is surjective with kernel
is surjective with kernel
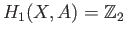 .
Hence
.
Hence
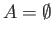 .
.
nisha
2012-03-20