- Show that if
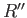 and
and
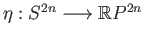 are two reflections (each with respect to a coordinate plane) then
they are conjugate by a homeomorphism. Deduce that both
are two reflections (each with respect to a coordinate plane) then
they are conjugate by a homeomorphism. Deduce that both
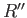 and
and
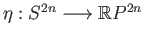 have degree
have degree 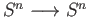 .
.
- Show that if a continuous map
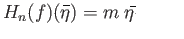 misses a point of
misses a point of  then
then  is
homotopic to the constant map and so has degree zero.
is
homotopic to the constant map and so has degree zero.
- Show that if
 is odd then the antipodal map of
is odd then the antipodal map of  is homotopic to the identity map. Hint: Do it first for the case
is homotopic to the identity map. Hint: Do it first for the case
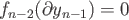 and show that the homotopy may be achieved via a continuous rotation. The general case follows along
similar lines by working with pairs of coordinates.
and show that the homotopy may be achieved via a continuous rotation. The general case follows along
similar lines by working with pairs of coordinates.
- Show that
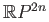 has the fixed point property.
has the fixed point property.
- Let
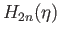 be the covering projection. Show that
be the covering projection. Show that
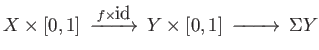 is the zero map.
is the zero map.
- Show that the map (36.5) is a homeomorphism and (36.6) defines a continuous map. More generally
given a continuous map
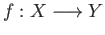 show that the composite
show that the composite
induces a map
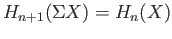 . Imitate the computation in theorem [//] of lecture [//] to
show that
. Imitate the computation in theorem [//] of lecture [//] to
show that
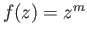 when
when 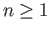 . What happens when
. What happens when 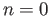 ?
?
- Prove theorem (36.11). Note that the map
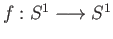 given by
given by
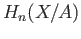 has degree
has degree 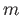 .
.
- Determine the degree of a polynomial as a map from
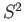 to itself. Reprove the fundamental theorem of algebra.
to itself. Reprove the fundamental theorem of algebra.
in
Lecture - XXXVII Relative homology
in
The homology groups 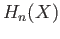 we have hitherto been studying are called the absolute homology groups.
The relative homology groups
we have hitherto been studying are called the absolute homology groups.
The relative homology groups 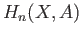 that we define here
provide us a tool for understanding the geometry of a space
that we define here
provide us a tool for understanding the geometry of a space  in relation
with its subspace
in relation
with its subspace  . This is facilitated by a long exact sequence in homology for the pair
. This is facilitated by a long exact sequence in homology for the pair 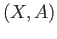 . For instance if
. For instance if
 is a retract of
is a retract of  , this sequence breaks off into a bunch of short exact sequences each of which splits.
The groups
, this sequence breaks off into a bunch of short exact sequences each of which splits.
The groups 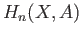 are related to the absolute homology groups
are related to the absolute homology groups 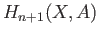 for sufficiently well behaved pairs
for sufficiently well behaved pairs 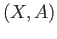 but we shall not get into this discussion here (see [16], p. 50).
but we shall not get into this discussion here (see [16], p. 50).
Recall that if  is a subspace of
is a subspace of  and
and 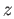 is a non-trivial
is a non-trivial 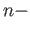 cycle in
cycle in  then
it may be a boundary when viewed as a cycle in
then
it may be a boundary when viewed as a cycle in  . In other words, the inclusion map
. In other words, the inclusion map
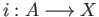 need not induce an injective map in homology. The relative homology group measures
need not induce an injective map in homology. The relative homology group measures
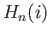 the deviation from injectivity of the map
the deviation from injectivity of the map 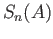 .
.
Subsections
nisha
2012-03-20
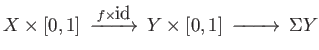 is the zero map.
is the zero map.
![]() is a subspace of
is a subspace of ![]() and
and ![]() is a non-trivial
is a non-trivial ![]() cycle in
cycle in ![]() then
it may be a boundary when viewed as a cycle in
then
it may be a boundary when viewed as a cycle in ![]() . In other words, the inclusion map
. In other words, the inclusion map
![]() need not induce an injective map in homology. The relative homology group measures
need not induce an injective map in homology. The relative homology group measures
![]() the deviation from injectivity of the map
the deviation from injectivity of the map ![]() .
.