For a pair 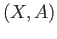 of spaces the connecting homomorphism
of spaces the connecting homomorphism
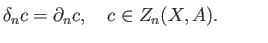 is given by
is given by
Despite the notation,
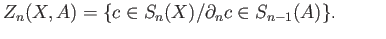 in (37.4) is not a boundary in
in (37.4) is not a boundary in
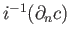 since
since 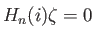 is not a chain in
is not a chain in 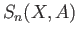 but a chain in
but a chain in 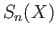 .
If
.
If 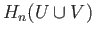 is a cycle in
is a cycle in  then for sure, it is a cycle in
then for sure, it is a cycle in  as well but then it may be actually be a
boundary
as well but then it may be actually be a
boundary  , in other words
, in other words
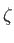 .
This happens precisely when
.
This happens precisely when
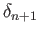 is in the image of
is in the image of
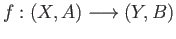 by exactness of (37.3). Figure below depicts a cycle in
by exactness of (37.3). Figure below depicts a cycle in  (annulus) which is a boundary in
(annulus) which is a boundary in  (the polygonal region).
in
The long exact sequence in the preceding theorem is natural in the following sense.
(the polygonal region).
in
The long exact sequence in the preceding theorem is natural in the following sense.
nisha
2012-03-20