next up previous
Next: Lemma 37.3: Up: Exercises Previous: Theorem 37.1:

Theorem 37.2:

For a pair 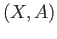$ (X, A)$ of topological spaces there is a long exact sequence in homology:

$\displaystyle \begin{CD} @> >> H_n(A) @> H_n(i)>> H_n(X) @> H_n(p)>> H_n(X, A) @> \delta_n >> H_{n-1}(A) @> >> \end{CD} \eqno(37.3) $

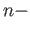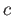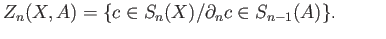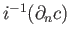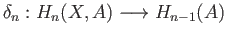We remark that the connecting homomorphism has a simple geometrical description in this case. If we take a relative $ n-$cycle namely an element $ c \in Z_n(X, A)$ then $ \partial _nc$ is an element of $ S_{n-1}(A)$ and $ i^{-1}(\partial _nc)$ is simply 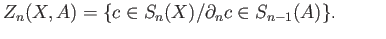$ \partial _nc$ viewed as a chain in $ A$. We summarize this observation as a lemma:
nisha 2012-03-20