We begin by proving (ii) implies (iii). Note that  is injective and so
im
is injective and so
im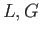 is isomorphic to
is isomorphic to  . Let
. Let 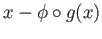 be arbitrary and observe that
be arbitrary and observe that
lies in the kernel of 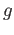 and hence in the image of
and hence in the image of  . Thus,
. Thus,
We leave it to the reader to check that the sum
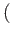 im
im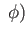 im
im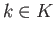 is direct.
It is easy to show that (iii) implies (i). We now show that (i) implies (ii). Let
is direct.
It is easy to show that (iii) implies (i). We now show that (i) implies (ii). Let 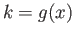 and choose any
and choose any
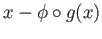 such that
such that 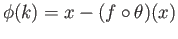 . Define
. Define
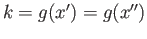 . To check that this is well defined, suppose
that
. To check that this is well defined, suppose
that
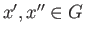 for a pair of elements
for a pair of elements
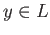 .
There exists
.
There exists 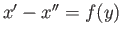 such that
such that
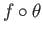 .
Applying
.
Applying
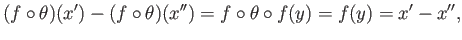 to this equation we get
to this equation we get
from which we see that
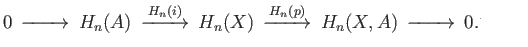 . It is trivial
to see that the map
. It is trivial
to see that the map  that we have defined is a group homomorphism and satisfies the requirement
that we have defined is a group homomorphism and satisfies the requirement
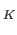 id
id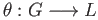 .
. 
nisha
2012-03-20