A short exact sequence of abelian groups/chain complexes
splits on the right if there exists a group homomorphism (respectively a chain map)
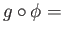 such that
such that
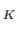 id
id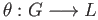 . The short exact sequence (37.6) splits on the left if there exists group homomorphism (respectively a chain map)
. The short exact sequence (37.6) splits on the left if there exists group homomorphism (respectively a chain map)
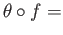 such that
such that
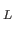 id
id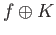 .
.
nisha
2012-03-20