We show that
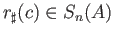 for every
for every  which would give us the sequences (37.7). For
which would give us the sequences (37.7). For
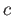 we have the chains
we have the chains
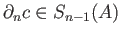 and
and
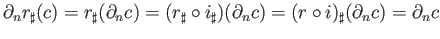 . Now,
. Now,
Hence
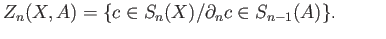 is the boundary of the chain
is the boundary of the chain
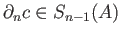 and so represents the zero element in
and so represents the zero element in
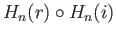 . From lemma (37.3) we conclude that
. From lemma (37.3) we conclude that 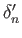 is the zero map.
The short exact sequence (37.7) splits on the left since
is the zero map.
The short exact sequence (37.7) splits on the left since
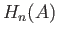 is the identity map on
is the identity map on 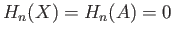 .
. 
nisha
2012-03-20