(i)
Given a topological space  and a subspace
and a subspace  ,
, 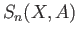 may be regarded as a
subgroup of
may be regarded as a
subgroup of 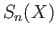 and
the group
and
the group 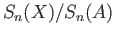 of relative
of relative 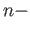 chains is the quotient group
chains is the quotient group
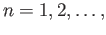 .
.
(ii) For each
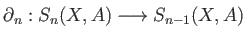 we define the boundary maps
we define the boundary maps
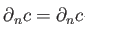 as
as
It is readily verified that
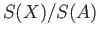 leading to the quotient complex
leading to the quotient complex
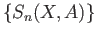 consisting of the sequence of groups
consisting of the sequence of groups
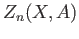 and the boundary maps (37.1).
and the boundary maps (37.1).
(iii) The homology groups of the quotient complex 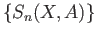 are called the relative
homology groups and are denoted by the
symbol
are called the relative
homology groups and are denoted by the
symbol 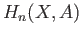 .
.
For a slightly more explicit description of these groups we introduce the group 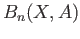 of relative
of relative 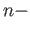 cycles and
the group
cycles and
the group 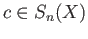 of relative boundaries.
The group
of relative boundaries.
The group 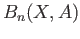 is the
subgroup of
is the
subgroup of 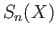 consisting of chains
consisting of chains
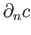 such that the boundary
such that the boundary
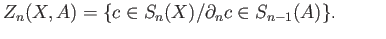 is a chain in
is a chain in  . That is,
. That is,
In keeping with the convention that
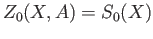 (see definition (29.5)),
(see definition (29.5)),
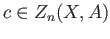 .
We see that
.
We see that
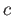 if and only if
if and only if
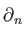 is in the kernel of
is in the kernel of
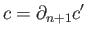 . Likewise the group
. Likewise the group
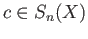 of relative boundaries is defined to be the subgroup of
of relative boundaries is defined to be the subgroup of 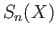 consisting of chains
consisting of chains
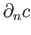 such that
such that
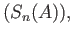
mod
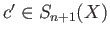
for some
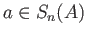 .
In other words there exists
.
In other words there exists
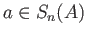 and
and
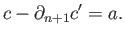 such that
such that
Obviously
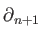 if and only if
if and only if
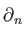 belongs to the image of
belongs to the image of
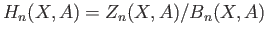 whereby we conclude
nisha
2012-03-20
whereby we conclude
nisha
2012-03-20
![]() we define the boundary maps
we define the boundary maps
![]() as
as
![]() are called the relative
homology groups and are denoted by the
symbol
are called the relative
homology groups and are denoted by the
symbol ![]() .
.
![]() of relative
of relative ![]() cycles and
the group
cycles and
the group ![]() of relative boundaries.
The group
of relative boundaries.
The group ![]() is the
subgroup of
is the
subgroup of ![]() consisting of chains
consisting of chains
![]() such that the boundary
such that the boundary
![]() is a chain in
is a chain in ![]() . That is,
. That is,