The long exact sequence for a pair and its naturality
gives a commutative diagram with exact rows.
Applying the excision theorem to the inclusion
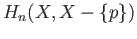 , we see that
the third arrow is an isomorphism in the displayed diagram. The result now follows from lemma (38.3).
, we see that
the third arrow is an isomorphism in the displayed diagram. The result now follows from lemma (38.3).
nisha
2012-03-20