- Prove that a homeomorphism
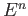 onto itself maps each boundary point of
onto itself maps each boundary point of 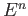 to a boundary point.
to a boundary point.
- Determine the homology groups of the Klein's bottle.
- Determine the homology groups of the double torus.
- Establish the isomorphism
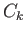 in the proof of theorem (35.4)
in the proof of theorem (35.4)
- Let
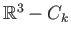 be the disjoint union of
be the disjoint union of 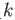 copies of
copies of 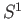 in
in
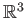 .
Determine the homology groups of the complement
.
Determine the homology groups of the complement
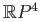 .
.
- Determine the homology groups of
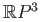 . Try computing the homology groups of
. Try computing the homology groups of
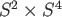 .
.
- Determine the homology groups of
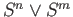 . Use exercise 4 of lecture 25.
to calculate the homology groups of
. Use exercise 4 of lecture 25.
to calculate the homology groups of
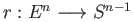 .
.
in
Lecture - XXXVI Maps of spheres
in
We are now in a position to prove the general Brouwer's fixed point theorem as well as a few other
surprising results concerning maps of spheres. As demonstrated in lecture 10, these higher dimensional
analogues were inaccessible via the theory of the fundamental group. We shall introduce the notion of the
degree of a map of spheres generalizing the notion introduced in lectures (12-13).
Subsections
nisha
2012-03-20