Since
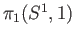 is abelian, the abelianization
is abelian, the abelianization
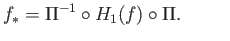 is an isomorphism and hence maps a generator of
is an isomorphism and hence maps a generator of
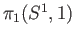 to a generator of
to a generator of 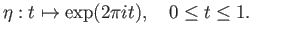 . Since (36.2) represents a generator for
. Since (36.2) represents a generator for
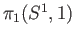 we infer that the cycle
(36.2) is a generator for
we infer that the cycle
(36.2) is a generator for 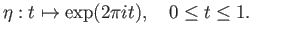 . We deduce from
the diagram (32.1) that
. We deduce from
the diagram (32.1) that
From (12.6) and (36.3) we see that
Appealing to the definition (36.1) we see that
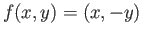 deg
deg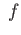 .
.
nisha
2012-03-20