The degree satisfies the following properties.
- (i)
- The degree of the identity map
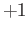 is
is 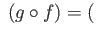 .
.
- (ii)
- If
 and
and 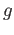 are two continuous maps from
are two continuous maps from  to itself then
deg
to itself then
deg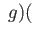 deg
deg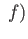 deg
deg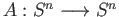 .
.
- (iii)
- Homotopic maps from
 into itself have the same degree.
into itself have the same degree.
- (iv)
- If
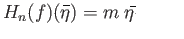 is a homotopy equivalence then degree of
is a homotopy equivalence then degree of  is
is 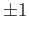 .
.
- (v)
- Any map homotopic to the constant map has degree zero.
- (vi)
- Any two maps
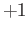 having the same degree are homotopic (Theorem of H. Hopf).
having the same degree are homotopic (Theorem of H. Hopf).
nisha
2012-03-20