From corollary (36.4) the case 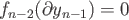 follows (exercise 1). The general case is done by induction.
Let us consider the covering
follows (exercise 1). The general case is done by induction.
Let us consider the covering 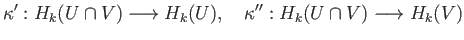 where
where
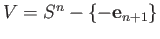 , and
, and
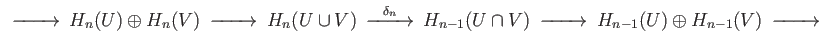 .
The map
.
The map 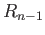 fixes
fixes  and
and  but when restricted to the equator
but when restricted to the equator  gives
gives 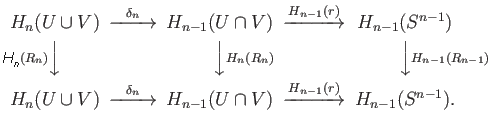 .
The naturality of the Mayer Vietoris sequence gives us the commutative diagram
The map
.
The naturality of the Mayer Vietoris sequence gives us the commutative diagram
The map
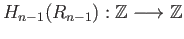 is isomorphism induced by the retraction of
is isomorphism induced by the retraction of 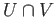 onto the equator
onto the equator  .
The connecting homomorphisms
.
The connecting homomorphisms 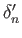 are isomorphisms as we have seen in the last lecture. Since the map
are isomorphisms as we have seen in the last lecture. Since the map
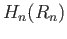 on the extreme right is given by multiplication by
on the extreme right is given by multiplication by 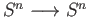 ,
the same is the case with the map
,
the same is the case with the map 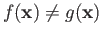 on the extreme left whereby we conclude that
on the extreme left whereby we conclude that 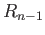 has degree
has degree 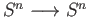 .
.
nisha
2012-03-20
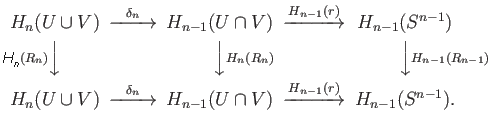 .
The naturality of the Mayer Vietoris sequence gives us the commutative diagram
.
The naturality of the Mayer Vietoris sequence gives us the commutative diagram