Suspension:

Given a topological space 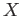$X$, the suspension of 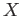$X$ denoted by 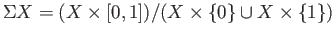$\Sigma X$, is obtained from $X\times [0,1]$ by passing to a quotient (see the figure that follows equation (36.6)):

$$\Sigma X =( X\times [0, 1])/(X\times \{0\} \cup X\times \{1\})$$

Using polar coordinates we can see that 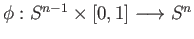$\Sigma S^{n-1} \cong S^n$ via the homeomorphism $\phi:S^{n-1}\times [0, 1]\longrightarrow S^n$

$$(\omega, t) \mapsto ((\sin\pi t)\;\omega, \cos \pi t),\quad t \in [0, 1],\;\; \omega \in S^{n-1}\subset \mathbb{R}^n. \eqno(36.5)$$

With this identification, given 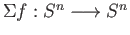$f:S^{n-1}\longrightarrow S^{n-1}$ continuous we define 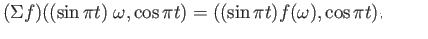$\Sigma f:S^n\longrightarrow S^n$ by

$$(\Sigma f)((\sin\pi t)\;\omega, \cos \pi t) = ((\sin\pi t)f(\omega), \cos \pi t) \eqno(36.6)$$

in