- For the map
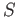 in example (18.3) show that
in example (18.3) show that 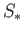 is the map
is the map
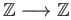 given by
given by
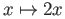 .
.
- Suppose
 is a path connected topological group with unit
element
is a path connected topological group with unit
element 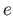 and
and
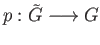 is a covering map.
For any choice of
is a covering map.
For any choice of
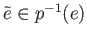 show that there is a group operation on
show that there is a group operation on
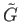 with unit element
with unit element
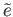 that makes
that makes
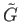 into a topological group and
into a topological group and  is a continuous group homomorphism.
is a continuous group homomorphism.
- Show that if
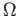 is an open subset of
is an open subset of
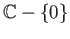 on which a
continuous branch of the logarithm exists then this branch is automatically holomorphic. Likewise show that
the continuous branch of
on which a
continuous branch of the logarithm exists then this branch is automatically holomorphic. Likewise show that
the continuous branch of
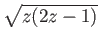 on
on
![$ \mathbb{C} - [0, 1/2]$](img1543.png) obtained in the lecture is
holomorphic.
obtained in the lecture is
holomorphic.
- Use the fact that
 is not a retract of
is not a retract of  to prove that
to prove that
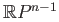 is not a retract of
is not a retract of
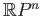 .
.
- Show that any continuous map
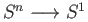 is homotopic to the constant map if
is homotopic to the constant map if 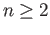 .
What about maps from the projective spaces
.
What about maps from the projective spaces
 (
(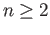 )?
)?
in
Lecture XIX - Deck Transformations
Given a covering projection
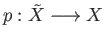 , the deck transformations are, roughly speaking,
the symmetries of the covering space. Thus it should not come as a surprise that they play a crucial part in the theory
of covering spaces. In this lecture all spaces are assumed to be
connected and locally path connected.
, the deck transformations are, roughly speaking,
the symmetries of the covering space. Thus it should not come as a surprise that they play a crucial part in the theory
of covering spaces. In this lecture all spaces are assumed to be
connected and locally path connected.
Subsections
nisha
2012-03-20
![]() , the deck transformations are, roughly speaking,
the symmetries of the covering space. Thus it should not come as a surprise that they play a crucial part in the theory
of covering spaces. In this lecture all spaces are assumed to be
connected and locally path connected.
, the deck transformations are, roughly speaking,
the symmetries of the covering space. Thus it should not come as a surprise that they play a crucial part in the theory
of covering spaces. In this lecture all spaces are assumed to be
connected and locally path connected.