Despite being an important theme,
we shall not discuss this in any detail in this elementary course but make a few remarks about it. Most of the
spaces that we shall encounter are reasonably well-behaved and indeed many of them such
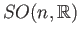 ,
, 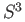 and the
projective spaces are smooth manifolds.
Given the existence of a simply connected covering -
called a universal
covering4,
one can develop a Galois correspondence for covering spaces which asserts the existence of
a unique (upto isomorphism) covering corresponding to each conjugacy class of subgroups of
and the
projective spaces are smooth manifolds.
Given the existence of a simply connected covering -
called a universal
covering4,
one can develop a Galois correspondence for covering spaces which asserts the existence of
a unique (upto isomorphism) covering corresponding to each conjugacy class of subgroups of
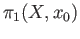 .
.
nisha
2012-03-20