Let us consider a fixed connected topological space  with a specified base point
with a specified base point 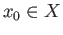 .
A homomorphism between two coverings
.
A homomorphism between two coverings
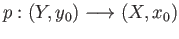 and
and
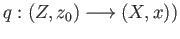 is a
surjective continuous map
is a
surjective continuous map
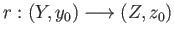 such that
such that
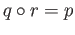 or diagrammatically,
or diagrammatically,
The definition enables us to form a category of coverings of a given space  with a specified base
point
with a specified base
point 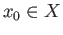 . To obtain a satisfactory theory one must impose some additional assumption on
. To obtain a satisfactory theory one must impose some additional assumption on  such as
local connectedness. In other words
such as
local connectedness. In other words 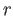 is a lift of
is a lift of  with respect to the covering map
with respect to the covering map 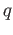 .
The universal covering is then defined in terms of a universal property.
.
The universal covering is then defined in terms of a universal property.
nisha
2012-03-20
![$\displaystyle \xymatrix{
(Y, y_0) \ar[rr]^{r}\ar[rd]_{p} & & (Z, z_0) \ar[ld]^{q}\\
& (X, x_0)
}
$](img1608.png)