Let
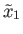 and
and
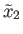 be two arbitrary points of
be two arbitrary points of
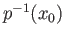 .
The action of Deck
.
The action of Deck
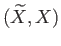 is transitive on
is transitive on
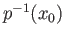 if and only if there is a
if and only if there is a
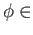 Deck
Deck
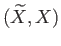 carrying
carrying
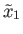 to
to
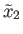 , which is the case if and only if
(19.1) holds. This in turn implies that the conjugacy class
, which is the case if and only if
(19.1) holds. This in turn implies that the conjugacy class
reduces to a singleton and conversely, in other words, if and only if the covering is regular. 
We now relate the (perhaps intransitive) action of Deck
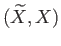 on
on
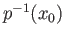 with the
transitive action of
with the
transitive action of
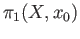 on
on
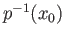 . Pick
. Pick 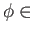 Deck
Deck
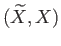 and
and
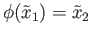 . Then on the one hand (19.1) must hold while since
. Then on the one hand (19.1) must hold while since
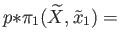 stab
stab
 (for the action of
(for the action of
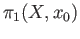 ),
we have on the other hand
),
we have on the other hand
for some
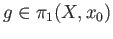 . In fact (19.2) states that
. In fact (19.2) states that 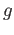 belongs to the normalizer
belongs to the normalizer
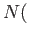
stab
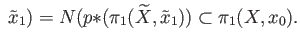
This suggests that we must relate  to the element
to the element
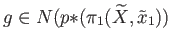 . However since there may be several such elements
. However since there may be several such elements 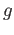 it is expedient
to define the map in the opposite direction.
it is expedient
to define the map in the opposite direction.
Let
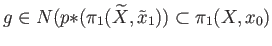 and
and
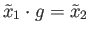 . Then (19.1) holds since
. Then (19.1) holds since 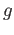 is in the normalizer of
stab
is in the normalizer of
stab
 . There is a unique
. There is a unique
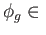 Deck
Deck
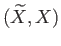 such that
such that
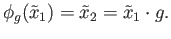 The map
The map
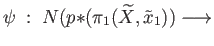
Deck
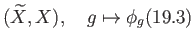
is a homomorphism. To see that it is surjective, let
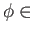 Deck
Deck
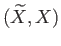 . There is a
. There is a
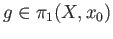 such that
such that
then stab
 and stab
and stab
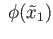 are conjugate by
are conjugate by 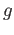 but they are also equal
by (iii) of Theorem (19.1), whereby we conclude
but they are also equal
by (iii) of Theorem (19.1), whereby we conclude 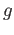 is in the normalizer
is in the normalizer
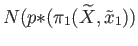 and
and
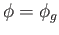 . To determine the kernel of
. To determine the kernel of 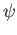 ,
observe that
,
observe that
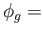 id if and only if
id if and only if
that is, if and only if
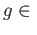 stab
stab
 . But stab
. But stab
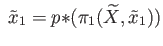 .
Summarizing these observations,
nisha
2012-03-20
.
Summarizing these observations,
nisha
2012-03-20
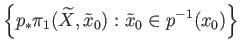
![]() on
on
![]() with the
transitive action of
with the
transitive action of
![]() on
on
![]() . Pick
. Pick ![]() Deck
Deck
![]() and
and
![]() . Then on the one hand (19.1) must hold while since
. Then on the one hand (19.1) must hold while since
![]() stab
stab
![]() (for the action of
(for the action of
![]() ),
we have on the other hand
),
we have on the other hand
![]() and
and
![]() . Then (19.1) holds since
. Then (19.1) holds since ![]() is in the normalizer of
stab
is in the normalizer of
stab
![]() . There is a unique
. There is a unique
![]() Deck
Deck
![]() such that
such that
![]() The map
The map