Statement (i) follows from the uniqueness of lifts.
Statement (ii) follows immediately from
the definition. To prove (iii) apply the lifting criterion (necessity) to both  and
and 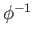 .
To prove (iv) apply lifting criterion (sufficiency) to get continuous functions
.
To prove (iv) apply lifting criterion (sufficiency) to get continuous functions
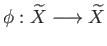 and
and
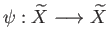 such that
such that
Then
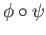 and
and
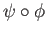 are both lifts of the map
are both lifts of the map
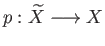 such that
such that
The identity map on
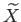 is also a lift of
is also a lift of  with these initial conditions. By uniqueness,
we see that both
with these initial conditions. By uniqueness,
we see that both
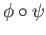 and
and
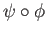 must be the identity map on
must be the identity map on
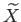 proving that
proving that
 and
and 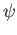 are homeomorphisms. The uniqueness clause follows from the
uniqueness of lifts.
are homeomorphisms. The uniqueness clause follows from the
uniqueness of lifts. 
nisha
2012-03-20