We fix a base
point 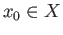 . Since each deck transformation is a bijection, it is a permutation of the fiber
. Since each deck transformation is a bijection, it is a permutation of the fiber
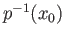 and so acts on
and so acts on
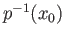 as a group of permutations:
as a group of permutations:
We study this action closely
and relate it to the action of
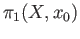 on the fiber
on the fiber
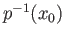 . We first look at the
case of regular coverings
. We first look at the
case of regular coverings
nisha
2012-03-20