Exercises

1. Suppose that a space $X$ has the fixed point property, is it necessary that it be connected? Does it have to be path-connected?
2. Explain why a non-trivial topological group cannot have the fixed point property.
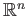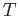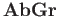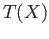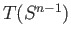3. Prove the Brouwer's fixed point theorem for the closed unit ball in $\mathbb{R}^n$ given that that there exists a functor $T$ from the category ${\bf Top}$ to the category ${\bf AbGr}$ such that $T(X)$ is the trivial group for every convex subset $X$ of a Euclidean space and $T(S^{n-1})$ is a non-trivial group.
4. Show that the Brouwer's fixed point theorem implies the no retraction theorem.
5. Explain how the homotopies 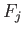$F_j$ in the proof of theorem 10.4 can be juxtaposed.
6. Show that the circle 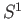$S^1$ is not a retract of the sphere $S^2$.

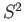in

Lecture XI - Homotopies of maps. Deformation retracts.

in We generalize the notion of homotopy of paths to homotopy of a pair of continuous maps between topological spaces. This would be particularly useful in the second part of the course. It also leads to a powerful notion of deformation retracts which is often useful in deciding whether two spaces have the same fundamental group. Homotopy of maps is a useful coarsening of the notion of homeomorphism of two spaces leading to the notion of homotopy equivalence of spaces. Over the decades homotopy has proved to be the most important notion in topology, susceptible to considerable generalization with wide applicability.