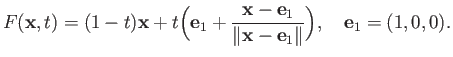Let 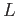 be the line
be the line
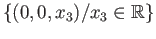 in
in
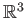 and
and
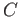 be the circle
be the circle
We show that the torus is a deformation retract of the space
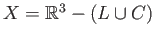 .
The idea is simple but some
details ought to be examined. Let us begin with the punctured half plane
.
The idea is simple but some
details ought to be examined. Let us begin with the punctured half plane
which clearly deformation retracts to the circle 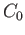 given by
given by
The homotopy
![$ F:H_0^{\prime}\times [0, 1]\longrightarrow H_0^{\prime}$](img954.png) is simply given by the convex combination:
is simply given by the convex combination:
The idea is to rotate the picture about the 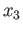 -axis. It is expedient to use spherical polar coordinates given by
-axis. It is expedient to use spherical polar coordinates given by
Let
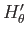 be the half plane bounded by the
be the half plane bounded by the 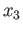 -axis making angle
-axis making angle 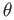 with
with
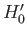 and
and
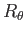 denote the rotation about the
denote the rotation about the 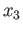 -axis mapping
-axis mapping
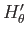 onto
onto
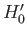 namely,
namely,
The homotopy we are looking for is then the map
![$ G:X\times [0,1]\longrightarrow X$](img963.png) given by
given by
It is easy to see using the properties of rotations, that
- (i)
 is well defined, that is the image of
is well defined, that is the image of  avoids the circle
avoids the circle 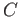
- (ii)
- Satisfies the requisite boundary conditions at
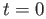 and
and 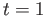 .
.
However,
the continuity of  is not automatic since the
is not automatic since the 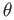 appearing in the definition of
appearing in the definition of  depends also
on
depends also
on 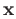 and we know that
and we know that 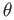 cannot be defined as a continuous function of
cannot be defined as a continuous function of 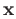 on
on  . One can either write
a formula (which is easy) and see that
. One can either write
a formula (which is easy) and see that 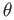 occurs in (11.8) only as
occurs in (11.8) only as
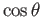 and
and
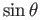 which are
continuous functions on
which are
continuous functions on  or better still use the property of quotients. We leave the amusing details to the reader.
nisha
2012-03-20
or better still use the property of quotients. We leave the amusing details to the reader.
nisha
2012-03-20