There exists
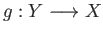 such that
such that 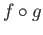 and
and 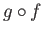 are respectively homotopic to
id
are respectively homotopic to
id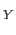 and
id
and
id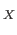 . By theorem 11.5
. By theorem 11.5
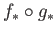 differs from the identity map on
differs from the identity map on
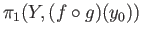 by a composition
with the isomorphism
by a composition
with the isomorphism
![$ h_{[\sigma]}$](img586.png) where
where  is a path joining
is a path joining 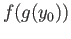 and
and 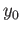 . In particular
. In particular
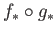 is bijective and so
is bijective and so
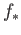 is surjective and
is surjective and 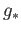 is injective. Likewise, working with
is injective. Likewise, working with 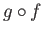 one concludes that
one concludes that 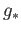 is surjective and
is surjective and 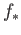 is injective.
Hence
is injective.
Hence 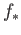 is an isomorphism between
is an isomorphism between
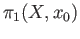 and
and
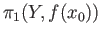 .
.
nisha
2012-03-20