Proof:

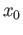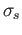The idea of proof is simple. Observe that (11.3) is the image of the base point $x_0$ under the deformation suggesting the use of theorem (7.8). If we fix an intermediate time $s\in [0,1]$ then the curve $\sigma_s$ given by 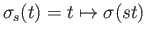$\sigma_s(t) = t \mapsto\sigma(st)$ starts at 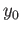$y_0$ and we could use it to construct a loop at 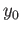$y_0$ namely

$$\sigma_s*F(\gamma(\;.\;), s)*\sigma_s^{-1}$$

In detail, for each loop 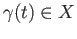$\gamma(t) \in X$ based at 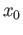$x_0$, the homotopy $\phi:[0, 1]\times [0, 1] \longrightarrow Y$ given by

$$\phi(s, t) = \sigma(3st)\; 0 \leq t \leq 1/3$$

$$= F(\gamma(3t-1), s)\; 1/3\leq t\leq 2/3$$

$$= \sigma(3s-3st)\; 2/3 \leq t\leq 1.$$

establishes the equality of $f_*[\gamma]$ and $[\sigma](g_{*}[\gamma])[\sigma^{-1}]$.