(i) Given continuous maps
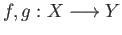 between topological spaces we say that
between topological spaces we say that  and
and 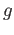 are homotopic if there
exists a continuous map
are homotopic if there
exists a continuous map
![$ F : X\times [0, 1] \longrightarrow Y$](img882.png) such that
such that
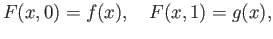
for all
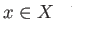
We shall occasionally use the notation 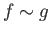 to indicate that
to indicate that  and
and 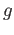 are homotopic.
One can formulate a notion for pairs of spaces:
are homotopic.
One can formulate a notion for pairs of spaces:
(ii) Two continuous maps
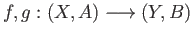 between pairs of topological spaces are said to be homotopic if there
exists
between pairs of topological spaces are said to be homotopic if there
exists
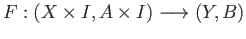 such that in addition to (11.1) the following condition holds:
such that in addition to (11.1) the following condition holds:
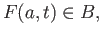
for all
![$\displaystyle a \in A, t \in [0, 1]. \eqno(11.2)
$](img889.png)
Condition (11.2) is a boundary condition which states that the intermediate functions
all map  into
into 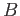 .
Note that when
.
Note that when
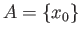 and
and
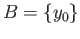 , the condition says that all the intermediate maps
, the condition says that all the intermediate maps
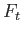 are base point preserving. We leave it to the reader to prove the following two simple results.
are base point preserving. We leave it to the reader to prove the following two simple results.
nisha
2012-03-20
![]() between pairs of topological spaces are said to be homotopic if there
exists
between pairs of topological spaces are said to be homotopic if there
exists
![]() such that in addition to (11.1) the following condition holds:
such that in addition to (11.1) the following condition holds: