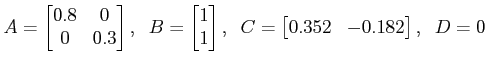Module 7 : Discrete State Space Models

Lecture 2 : State Space Model to Transfer Function

When the matrix $ A$ has repeated eigenvalues, it cannot be expressed in a proper diagonal form. However, it can be expressed in a Jordan canonical form which is nearly a diagonal matrix. Let us consider that the system has eigenvalues, $ \lambda_1$, $ \lambda_1$, $ \lambda_2$ and $ \lambda_3$. In that case, $ A$ matrix in Jordan canonical form will be

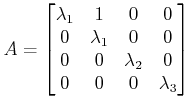
$\displaystyle A= \begin{bmatrix} \lambda_1 & 1 & 0 & 0\\ 0 & \lambda_1 & 0 & 0\\ 0 & 0 & \lambda_2 & 0\\ 0 & 0 & 0 & \lambda_3 \end{bmatrix} $

  1. The diagonal elements of the matrix 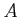$ A$ are eigenvalues of the same.


  2. The elements below the principal diagonal are zero.


  3. Some of the elements just above the principal diagonal are one.


  4. The matrix can be divided into a number of blocks, called Jordan blocks, along the diagonal. Each block depends on the multiplicity of the eigenvalue associated with it. For example, Jordan block associated with a eigenvalue 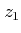$ z_1$ of multiplicity 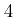$ 4$ can be written as

    $\displaystyle A= \begin{bmatrix} z_1 & 1 & 0 & 0\\ 0 & z_1 & 1 & 0\\ 0 & 0 & z_1 & 1\\ 0 & 0 & 0 & z_1 \end{bmatrix}$

Example: Consider the following discrete transfer function.

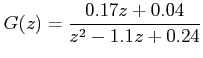
$\displaystyle G(z) = \frac{0.17z+0.04}{z^2-1.1z+0.24} $

Find out the state variable model in 3 different canonical forms.

Solution:

The state variable model in controllable canonical form can directly be derived from the transfer function, where the A, B, C and D matrices are as follows:

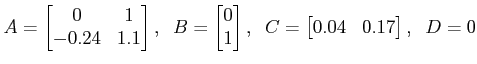
$\displaystyle A = \begin{bmatrix}0 & 1\\ -0.24 & 1.1 \end{bmatrix}, \;\; B = \b... ...\ 1 \end{bmatrix}, \;\; C = \begin{bmatrix}0.04 & 0.17 \end{bmatrix}, \;\; D=0 $

The matrices in state model corresponding to observable canonical form are obtained as,

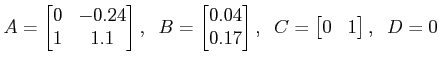
$\displaystyle A = \begin{bmatrix}0 & -0.24 \\ 1 & 1.1 \end{bmatrix}, \;\; B = \... ...4 \\ 0.17 \end{bmatrix}, \;\; C = \begin{bmatrix}0 & 1 \end{bmatrix}, \;\; D=0 $

 

To find out the state model in Jordan canonical form, we need to fact expand the transfer function using partial fraction, as

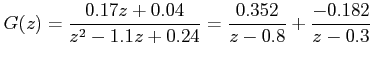
$\displaystyle G(z) = \frac{0.17z+0.04}{z^2-1.1z+0.24} = \frac{0.352}{z-0.8} + \frac{-0.182}{z-0.3}$

Thus the A, B, C and D matrices will be:

$\displaystyle A = \begin{bmatrix}0.8 & 0\\ 0 & 0.3 \end{bmatrix}, \;\; B = \beg... ... \end{bmatrix}, \;\; C = \begin{bmatrix}0.352 & -0.182 \end{bmatrix}, \;\; D=0 $