Choosing the outputs of the delay blocks as the state variables, we have following state equations

This can be rewritten in matrix form (4) with

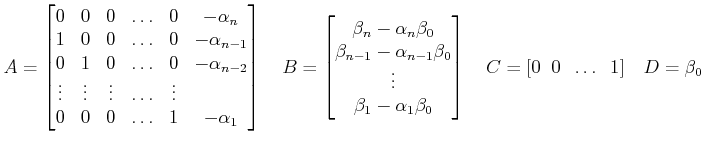
2.3 Duality

In previous two sections we observed that the system matrix A in observable canonical form is transpose of the system matrix in controllable canonical form. Similarly, control matrix B in observable canonical form is transpose of output matrix C in controllable canonical form. So also output matrix C in observable canonical form is transpose of control matrix B in controllable canonical form.

2.4 Jordan Canonical Form

In Jordan canonical form, the system matrix A represents a diagonal matrix for distinct poles which basically form the diagonal elements of A.

Assume that $z=\lambda_i, \;\; i=1,2, \ldots, n$ are the distinct poles of the given transfer function (3). Then partial fraction expansion of the transfer function yields