where
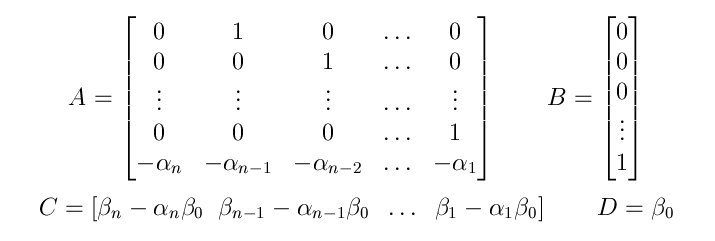
2.2 Observable Canonical Form
Equation (3) may be rewritten as
![$\displaystyle \textrm{or,} \; z^n[Y(z)-\beta_0U(z)]+z^{n-1}[\alpha_1Y(z)-\beta_1U(z)]+\ldots+[\alpha_nY(z)-\beta_nU(z)]=0$](images/img39.png){kind=small}
![$\displaystyle \textrm{or,} \; Y(z)=\beta_0U(z)+ {z}^{-1}[\alpha_1Y(z)-\beta_1U(z)]+\ldots+z^{-n}[\alpha_nY(z)-\beta_nU(z)]$](images/img40.png){kind=small}
The corresponding block diagram is shown in Figure 2.
 |
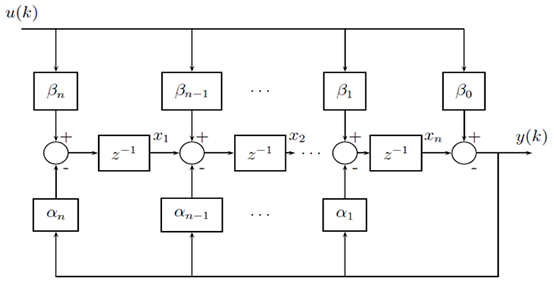Figure 2: Block Diagram representation of observable canonical form |
Module 7 : Discrete State Space Models
Lecture 2 : State Space Model to Transfer Function
where
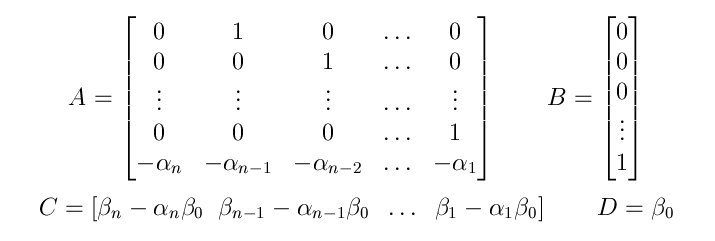
Equation (3) may be rewritten as
The corresponding block diagram is shown in Figure 2.
|
Figure 2: Block Diagram representation of observable canonical form |