Laplace transform of sampled signal r*(t) is

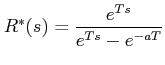
$\displaystyle R^{*}(s)=\frac{e^{Ts}}{e^{Ts}-e^{-aT}}$

Laplace transform of the output after the ZOH is

$\displaystyle H(s)$	$\displaystyle =$	$\displaystyle G_{ho}(s)R^{*}(s)$
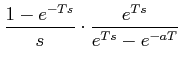	$\displaystyle =$	$\displaystyle \frac{1-e^{-Ts}}{s} \cdot \frac{e^{Ts}}{e^{Ts}-e^{-aT}}$

When T → 0 ,

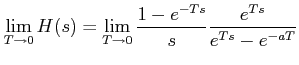
$\displaystyle \lim_{T\rightarrow 0}H(s)=\lim_{T\rightarrow 0}\frac{1-e^{-Ts}}{s}\frac{e^{Ts}}{e^{Ts}-e^{-aT}}$

The limit can be calculated using L' hospital's rule. It says that:

If $\displaystyle \lim_{x\rightarrow a}f(x)=0/\infty$ and if $\displaystyle \lim_{x\rightarrow a} g(x)=0/\infty$ , then

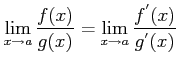
$\displaystyle \lim_{x\rightarrow a} \frac {f(x)}{g(x)}=\lim_{x\rightarrow a}\frac {f^{'}(x)}{g^{'}(x)}$

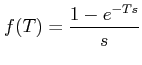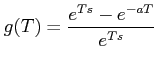For the given example, x = T, $f(T)=\dfrac{1-e^{-Ts}}{s}$ and $g(T)=\dfrac{e^{Ts}-e^{-aT}}{e^{Ts}}$ . Both the expressions approach zero as T → 0. So,

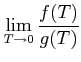$\displaystyle H(s)$	$\displaystyle =$	$\displaystyle \lim_{T\rightarrow 0} \frac {f(T)}{g(T)}$
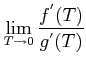	$\displaystyle =$	$\displaystyle \lim_{T\rightarrow 0} \frac {f^{'}(T)}{g^{'}(T)}$
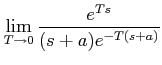	$\displaystyle =$	$\displaystyle \lim_{T\rightarrow 0} \frac{e^{Ts}}{(s+a)e^{-T(s+a)}}$
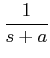	$\displaystyle =$	$\displaystyle \frac{1}{s+a}$
	$\displaystyle =$	$\displaystyle R(s)$

which implies that the original signal can be recovered from the output of the sample and hold device if the sampling period approaches zero.