One can then write:

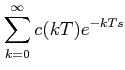$\displaystyle C^{*}(s)$	$\displaystyle =$	$\displaystyle \sum_{k=0}^{\infty}c(kT)e^{-kTs}$
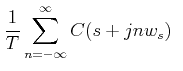Since c(kT) is periodic, $\displaystyle \; C^{*}(s)$	$\displaystyle =$	$\displaystyle \frac{1}{T} \sum_{n=-\infty}^{\infty}c(s+jnw_{s}) \;\;$ with c(0) = 0

The detailed derivation of the above expression is omitted. Similarly,

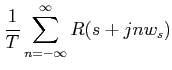$\displaystyle R^{*}(s)$	$\displaystyle =$	$\displaystyle \frac{1}{T} \sum_{n=-\infty}^{\infty}R(s+jnw_{s})$
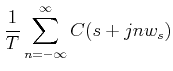Again, $\displaystyle \; C^{*}(s)$	$\displaystyle =$	$\displaystyle \frac{1}{T} \sum_{n=-\infty}^{\infty}c(s+jnw_{s})$
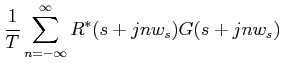	$\displaystyle =$	$\displaystyle \frac{1}{T} \sum_{n=-\infty}^{\infty}R^*(s+jnw_{s})G(s+jnw_{s})$

Since R*(s) is periodic R*( s + jnw_s) = R*(s). Thus

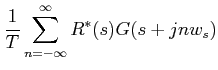$\displaystyle C^{*}(s)$	$\displaystyle =$	$\displaystyle \frac{1}{T}\sum_{n=-\infty}^{\infty}R^{*}(s)G(s+jnw_{s})$
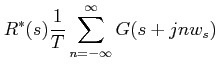	$\displaystyle =$	$\displaystyle R^{*}(s) \frac{1}{T}\sum_{n=-\infty}^{\infty}G(s+jnw_{s})$

If we define

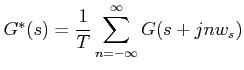$G^{*}(s)= \displaystyle \frac{1}{T}\sum_{n=-\infty}^{\infty}G(s+jnw_{s})$ , then $C^{*}(s)=R^{*}(s)G^{*}(s)$ .

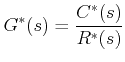
$\displaystyle G^{*}(s)=\frac{C^*(s)}{R^*(s)}$

is known as pulse transfer function. Sometimes it is also referred to as the starred transfer function.

If we now substitute z = e^Ts in the previous expression, we will directly get the z-transfer function G(z) as

$\displaystyle G(z)$

$\displaystyle =$

$\displaystyle \frac {C(z)}{R(z)}$