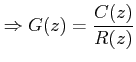G(z) can also be defined as

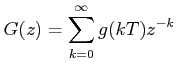
$\displaystyle G(z)=\sum_{k=0}^{\infty}g(kT)z^{-k}$

where g(kT) denotes the sequence of the impulse response g(t) of the system of transfer function G(s). The sequence g(kT), k = 0, 1, 2,... , is also known as impulse sequence.

Overall Conclusion

1. Pulse transfer function or Z transfer function characterizes the discrete data system only at sampling instants. The output information between the sampling instants is lost.

2. Since the input of discrete data system is described by output of the sampler, for all practical purposes, the samplers can be simply ignored and the input can be regarded as r*(t).

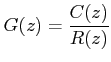Alternate way to arrive at $G(z)=\dfrac{C(z)}{R(z)}$ :

$\displaystyle c^{*}(t)$	$\displaystyle =$	$\displaystyle g^{}(t) \big \vert _{\text{when $r^{}(t)$\ is an impulse response}}$
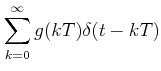	$\displaystyle =$	$\displaystyle \sum_{k=0}^{\infty}g(kT)\delta (1-kT)$

When the input is r*(t),

$\displaystyle c(t)$	$\displaystyle =$	$\displaystyle r(0)g(t)+r(T)g(t-T)+...$
$\displaystyle \Rightarrow c(kT)$	$\displaystyle =$	$\displaystyle r(0)g(kT)+r(T)g((k-1)T)+...$
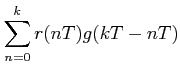$\displaystyle \Rightarrow c(kT)$	$\displaystyle =$	$\displaystyle \sum_{n=0}^{k}r(nT)g(kT-nT)$
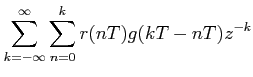$\displaystyle \Rightarrow C(z)$	$\displaystyle =$	$\displaystyle \sum_{k=-\infty}^{\infty} \sum_{n=0}^{k}r(nT)g(kT-nT)z^{-k}$

Using real convolution theorem

$\displaystyle C(z)=R(z)G(z)$

$\displaystyle \Rightarrow G(z)=\frac {C(z)}{R(z)}$