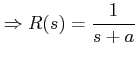Z-transform of output c(t) is

$\displaystyle C(z)$	$\displaystyle =$	$\displaystyle Z\left[G_{oh}(s)G(s)\right]R(z)$
	$\displaystyle =$	$\displaystyle Z\left[\frac{1-e^{-Ts}}{s}G(s)\right]R(s)$
	$\displaystyle =$	$\displaystyle (1-z^{-1})Z\left[\frac{G(s)}{s}\right]R(z)$

where $\displaystyle (1-z^{-1})Z\left[\frac{G(s)}{s}\right]$ is the Z-transfer function of an S/H device and a linear system.

It was mentioned earlier that when sampling frequency reaches infinity, a discrete data system may be regarded as a continuous data system. However, this does not mean that if the signal r(t) is sampled by an ideal sampler then r*(t) can be reverted to r(t) by setting the sampling time T to zero. This simply bunches all the samples together. Rather, if the output of the sampled signal is passed through a hold device then setting the sampling time T to zero the original signal r(t) can be recovered. In relation with Figure 2,

$\displaystyle \lim_{T\rightarrow 0}H(s)=R(s)$

Example
Consider that the input is $r(t)=e^{-at}u_{s}(t)$ , where $u_{s}(t)$ is the unit step function.

$\displaystyle \Rightarrow R(s)=\frac {1}{s+a}$