1.1 Pluse transfer function of ZOH

As derived in lecture 4 of module 1, transfer function of zero order hold is

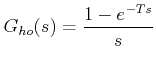$\displaystyle G_{oh}(s)= \frac {1-e^{-Ts}}{s}$
$\displaystyle \Rightarrow$ Pulse transfer function $\displaystyle \;\; G_{oh}(z)$	$\displaystyle =$	$\displaystyle Z\left[\frac {1-e^{-Ts}}{s}\right]$
	$\displaystyle =$	$\displaystyle (1-z^{-1})Z\left[\frac{1}{s}\right]$
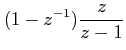	$\displaystyle =$	$\displaystyle (1-z^{-1})\frac {z}{z-1}$
	$\displaystyle =$	$\displaystyle 1$

This result is expected because zero order hold simply holds the discrete signal for one sampling period, thus taking Z-transform of ZOH would revert back its original sampled signal.

A common situation in discrete data system is that a sample and hold (S/H) device precedes a linear system with transfer function G(s) as shown in Figure 2. We are interested in finding the transform relation between r*(t) and c*(t).

**Figure 2:** Block diagram of a system subject to a sample and hold process
$\begin{figure}\centering \input{m2fig2.pstex_t}\end{figure}$