| |
Cylnidrical coordinate system is obtained by extending the polar coordinates by adding a z-axis along the height of a right circular cylinder. The z-axis of the coordinate system is same as that in a cartesian system. |
| |
In the figure 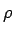 is the distance of the foot of the perpendicular drawn from the point to the is the distance of the foot of the perpendicular drawn from the point to the 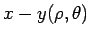 plane. Note that plane. Note that 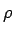 here is not the distance of the point P from the origin, as is the case in polar coordinate systems. (Some texts use here is not the distance of the point P from the origin, as is the case in polar coordinate systems. (Some texts use 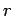 to denote what we are calling as to denote what we are calling as 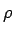 here. However, we use here. However, we use 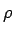 to denote the distance from the origin to the foot of the perpendicular to avoid confusion.) In terms of cartesian coordinates to denote the distance from the origin to the foot of the perpendicular to avoid confusion.) In terms of cartesian coordinates |
| |
so that the inverse relationships are |