| |
When we transform from one coordinate system to another, the differential element also transform. |
| |
For instance, in 2 dimension the element of an area is 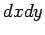 but in polar coordinates the element is not but in polar coordinates the element is not 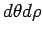 but but 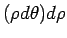 . This extra factor . This extra factor 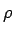 is important when we wish to integrate a function using a different coordinate system. is important when we wish to integrate a function using a different coordinate system. |
| |
If 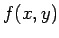 is a function of is a function of 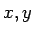 we may express the function in polar coordinates and write it as we may express the function in polar coordinates and write it as 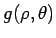 . However, when we evaluate the integral . However, when we evaluate the integral 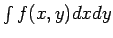 in polar coordinates, the corresponding integral is in polar coordinates, the corresponding integral is 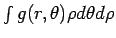 . In general, if . In general, if 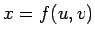 and and 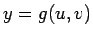 , then, in going from , then, in going from 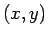 to to 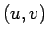 , the differential element , the differential element 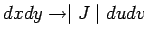 where where 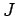 is given by the determinant is given by the determinant |
| |
The differentiations are partial, i.e., while differentiating 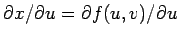 , the variable , the variable 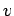 is treated as constant. An useful fact is that the Jacobian of the inverse transformation is is treated as constant. An useful fact is that the Jacobian of the inverse transformation is 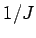 because the detrminant of the inverse of a matrix is equal to the inverse of the determinant of the original matrix. because the detrminant of the inverse of a matrix is equal to the inverse of the determinant of the original matrix. |