| |
Spherical coordinates are useful in dealing with problems which possess spherical symmetry. The independent variables of the system are 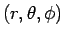 . Here . Here 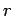 is the distance of the point is the distance of the point 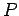 from the origin. Angles from the origin. Angles 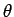 and and 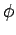 are similar to latitudes and longitudes. are similar to latitudes and longitudes.
Two mutually perpendicular lines are chosen, taken to coincide with the x-axis and z-axis of the cartesian system. We take angle 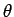 to be the angle made by the radius vector (i.e. the vector connecting the origin to P) with the z-axis (the angle to be the angle made by the radius vector (i.e. the vector connecting the origin to P) with the z-axis (the angle 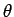 is actually complementary to the latitude). The angle is actually complementary to the latitude). The angle 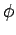 is the angle between the x-axis and the line joining the origin to is the angle between the x-axis and the line joining the origin to 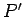 , the foot of the perpendicular from , the foot of the perpendicular from 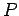 to the x-y plane. to the x-y plane.
The unit vectors 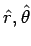 and and 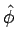 are respectively along the directions of increasing are respectively along the directions of increasing 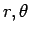 and and 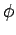 . .
|