| |
Relationship with the cartesian components are |
| |
so that the inverse relationships are |
| |
By definition, the distance 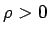 . we will take the range of angles . we will take the range of angles 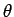 to be to be 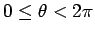 (It is possible to define the range to be (It is possible to define the range to be 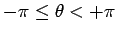 ). One has to be careful in using the inverse tangent as the arc-tan function is defined in ). One has to be careful in using the inverse tangent as the arc-tan function is defined in 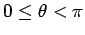 . If . If 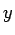 is negative, one has to add is negative, one has to add 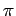 to the principal value of to the principal value of 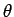 calculated by the arc - tan function so that the point is in proper quadrant. calculated by the arc - tan function so that the point is in proper quadrant. |