| |
Differentiation of polar unit vectors with respect to time : |
| |
It may be noted that the basis vectors 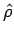 and and 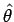 , unlike , unlike 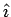 and and 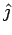 are not constant vectors but depend on the position of the point. The time derivative of the unit vectors are defined as follows are not constant vectors but depend on the position of the point. The time derivative of the unit vectors are defined as follows |
| |
One can evaluate the derivatives by laborious process of expressing the unit vectors 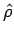 and and 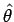 in terms of constant unit vectors of cartesian system, differentiating the resulting expressions and finally transform back to the polar form. Alternatively, we can look at the problem geometrically, as shown in the following figure. in terms of constant unit vectors of cartesian system, differentiating the resulting expressions and finally transform back to the polar form. Alternatively, we can look at the problem geometrically, as shown in the following figure. |