| |
The differential element of volume is obtained by constructing a closed volume by extending 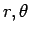 and and 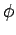 respectively by respectively by 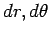 and and 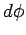 . The length elements in the direction of . The length elements in the direction of 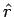 is dr, that along is dr, that along 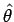 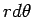 while that along while that along 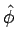 is is 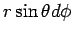 (see figure). The volume element, therefore, is (see figure). The volume element, therefore, is |
| |
Thus the Jacobian of transformation is 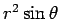 . . |