| |
In the figure, the positions of a particle are shown at time 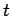 and and 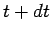 . The unit vectors . The unit vectors 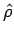 is shown in red while the unit vector is shown in red while the unit vector 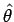 is shown in blue. It can be easily seen by triangle law of addition of vectors that the magnitude of is shown in blue. It can be easily seen by triangle law of addition of vectors that the magnitude of 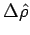 and and 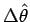 is is 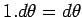 . However, as the limit . However, as the limit 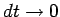 , the direction of , the direction of 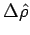 is in the direction of is in the direction of 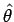 while that of while that of 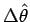 is in the direction of is in the direction of 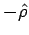 . Thus . Thus |
| |
Now, 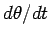 is the angular velocity of the point, which is usually denoted by is the angular velocity of the point, which is usually denoted by 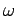 , Thus we have, , Thus we have, |