| Realizations of Digital Filters |
We have many realizations
of digital filter. Some of these are now discussed. Direct
Form Realization - An important class
of linear time -invariant systems is characterized
by the transfer function.
|
| |
A system with input 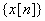 and
output and
output 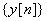 could
be realized by the following constant coefficient
difference equation could
be realized by the following constant coefficient
difference equation
|
| |
A realization of
the filter using equation (9.31) is shown in
figure (9.6)
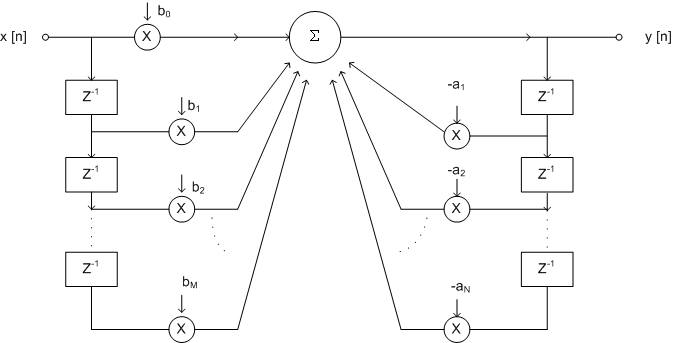
Fig 9.6 Direct form I
|
The output 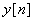 is
seen to be weighted sum of input is
seen to be weighted sum of input 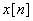 and
past inputs and
past inputs 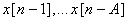 and
past outputs.
Another realization can be obtained by uniting and
past outputs.
Another realization can be obtained by uniting 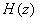 as
product of two transfer functions as
product of two transfer functions 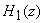 and and 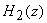 ,
where ,
where 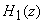 contains
only the denominator or poles and contains
only the denominator or poles and 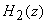 contains
only the numerator or zeros as follows contains
only the numerator or zeros as follows |
| |
where |
| |
| |
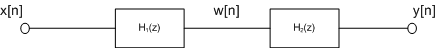
Fig 9.7
|
The output of the
filter is obtained by calculating the intermediate
result 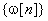 obtained
from operating on the input with filter obtained
from operating on the input with filter 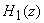 and
then operating on w[n] with
filter.Thus
we obtain and
then operating on w[n] with
filter.Thus
we obtain |
| |
or |
| |
and |
| |
or |
| |
The realization is
shown in figure 9.8
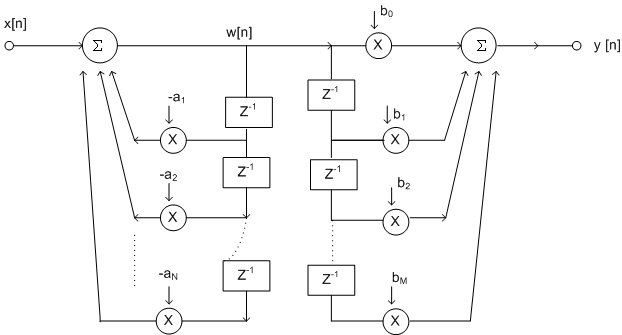
Fig 9.8
|
Upon close examination
of Fig 9.8, it can be seen that the two branches
of delay elements can be combined as they both
refer to delayed versions of 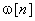 and
upon simplification, the direct form II canonical
realization is obtained as shown in figure 9.9. and
upon simplification, the direct form II canonical
realization is obtained as shown in figure 9.9.
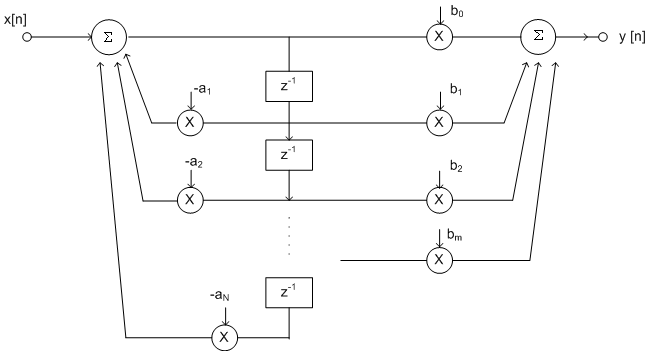
Fig 9.9 Direct form
II
|
In this form the
number of delay element is max (M,N). It can
be shown that this is the minimum number of delay
elements that are required to implement the digital
filter. This does not mean that this is the best
realization. Immunity to roundoff and quantization
are very important considerations.
An important special case that is used as building
block occurs when.
Thus  is
ratio of two qualities in is
ratio of two qualities in  ,
called biquadratic section, and is given by ,
called biquadratic section, and is given by
|
| |
| |
The alternative form
is found to be useful for amplitude scaling for
improving performance file filter operation.
This form is shown in figure 9.10.
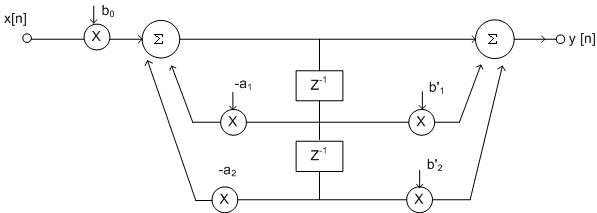
Fig 9.10
|
Cascade
Realizations: In
the cascade realization 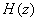 is
broken into productof transfer functions is
broken into productof transfer functions 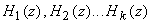 each
a rational expression in each
a rational expression in 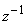 as
follows as
follows |
| |

Fig 9.11
|
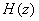 could
be broken up in many ways; however the most common
method is to use biquadratic sections. Thus could
be broken up in many ways; however the most common
method is to use biquadratic sections. Thus
|
| |
by letting 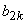 and and 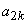 equal
to zero we get bilinear section. Even among the
biquadratic sections we have many choices as
how we pair poles and zeros. Also the order of
the sections can be different equal
to zero we get bilinear section. Even among the
biquadratic sections we have many choices as
how we pair poles and zeros. Also the order of
the sections can be different |
Example: |
| Final
cascade realization of |
| |
Using only real coefficients 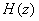 can
be decompressed as can
be decompressed as |
| |
Divides both numerator
and denominator by 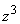 and
factoring 8 as and
factoring 8 as 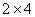 ,
one possible rearrangement for ,
one possible rearrangement for 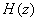 is is |
| |
This can be realized as shown is figure 9.12
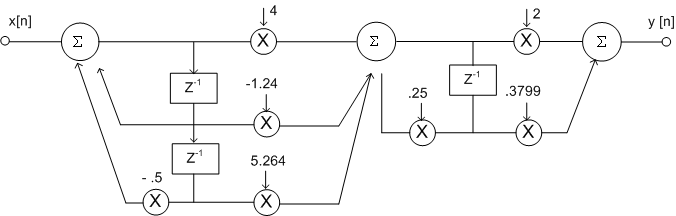
Fig 9.12
|
| |
| Parallel
Realizations: |
The transfer function H ( z )
could be written as a sum of transfer functions 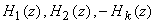 as
follows: as
follows: |
| |
One parallel form
results when 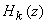 are
all selected to be of the following form for are
all selected to be of the following form for
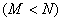 |
| |
If 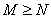 ,
we will have a section ,
we will have a section 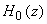 of
FIR filter, obtained by performing long division.
Once denominator polynomial has degree more than
the numerator polynomial we perform the partial
fraction expansion. The resulting structure is
shown in figure 9.13. of
FIR filter, obtained by performing long division.
Once denominator polynomial has degree more than
the numerator polynomial we perform the partial
fraction expansion. The resulting structure is
shown in figure 9.13.
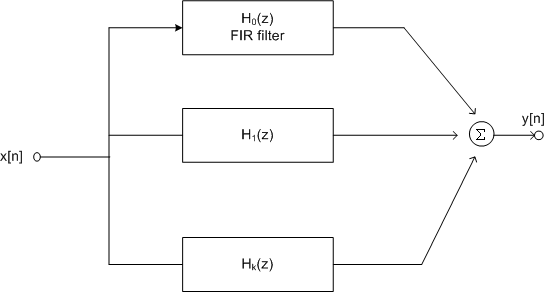
Fig 9.13
|
| Example: |
| Find the parallel form
for the filter given in last example. |
| |
Using MATLAB program or otherwise we get |
| |
using direst form
realization for individual section we get the
structure shown in figure 9.14.
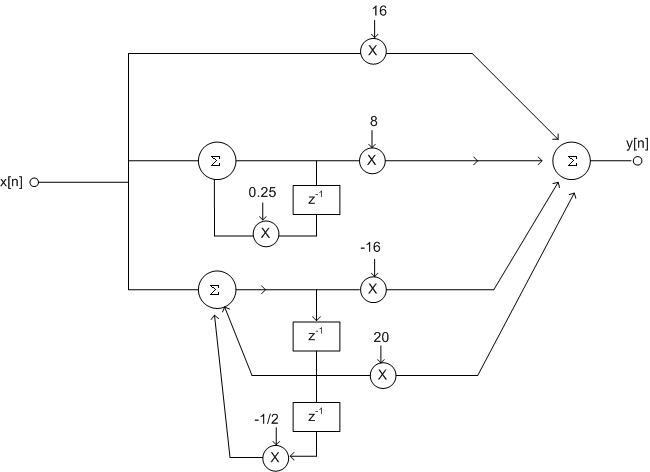
Fig 9.14
Apart from these there exist a number of other
realizations like lattice form, state variable
realization etc.
|
| |
| |