Design a lowpass
IIR digital filter H(z)
with maximally flat magnitude characteristics.
The passband edge frequency 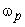 is is 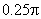 with
a passband ripple not exceeding 0.5dB. The minimum
stopband attenuation at the stopband edge frequency with
a passband ripple not exceeding 0.5dB. The minimum
stopband attenuation at the stopband edge frequency 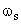 of of 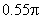 is
15 dB. is
15 dB.
We assume that no aliasing occurs. Taking 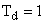 ,
the analog filter has ,
the analog filter has 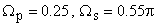 ,
the passband ripple is 0.5dB, and minimum stopped
attenuation is 15dB. For maximally flat frequency
response we choose Butterworth filter characteristics.
From passband ripple of 0.5 dB we get ,
the passband ripple is 0.5dB, and minimum stopped
attenuation is 15dB. For maximally flat frequency
response we choose Butterworth filter characteristics.
From passband ripple of 0.5 dB we get |